2014年03月30日
科学キャラクター図鑑
息子が最近楽しんでいるのが、
「科学キャラクター図鑑」(玉川大学出版部)です。

科学で扱う概念や物をキャラクターに喩え、
そのキャラクターが自己紹介する形で、
概念や物が説明されています。

たとえば、物理学の「重さ」では、
「重さ」ちゃんが、
「ぼくちゃんは話題の中心だよ。
ガリガリにやせたモデルたちから、太り過ぎの子どもたちまで、
みんな”重さ”を気にしているからさ。
でも、本当は、みんなは質量を気にしているんだよ。
物の中にたくさん物質が詰まっているかを教えてくれるのは、質量だからね。
ぼく(重さ)は、どんな力がそれに働いているかしか表していない。」
と自己紹介しています。
私が中学生の時に
先生にした質問 「質量」と「重さ」の違い への
先生の答えより断然わかりやすいです
内容は、物理学では、
ニュートン力学に始まり、
「シュレディンガー猫」「ヒッグス粒子」まで盛り沢山。
高校の物理で扱う概念までしっかりカバーしてあります。
息子は、キャラクターの自己紹介よりも
キャラクターの絵のおもしろさに惹かれ、
楽しんでいるようです。
息子のリクエストで、
「天文学」も購入してしまいました。
「科学キャラクター図鑑」(玉川大学出版部)です。

科学で扱う概念や物をキャラクターに喩え、
そのキャラクターが自己紹介する形で、
概念や物が説明されています。

たとえば、物理学の「重さ」では、
「重さ」ちゃんが、
「ぼくちゃんは話題の中心だよ。
ガリガリにやせたモデルたちから、太り過ぎの子どもたちまで、
みんな”重さ”を気にしているからさ。
でも、本当は、みんなは質量を気にしているんだよ。
物の中にたくさん物質が詰まっているかを教えてくれるのは、質量だからね。
ぼく(重さ)は、どんな力がそれに働いているかしか表していない。」
と自己紹介しています。
私が中学生の時に
先生にした質問 「質量」と「重さ」の違い への
先生の答えより断然わかりやすいです

内容は、物理学では、
ニュートン力学に始まり、
「シュレディンガー猫」「ヒッグス粒子」まで盛り沢山。
高校の物理で扱う概念までしっかりカバーしてあります。
息子は、キャラクターの自己紹介よりも
キャラクターの絵のおもしろさに惹かれ、
楽しんでいるようです。
息子のリクエストで、
「天文学」も購入してしまいました。
2013年07月08日
シャク

先日、
といっても、もう半月ばかり前に、
シャクをいただいので、から揚げにしました。
熊本の初夏の味を
冷酒をお供に堪能しました。
九州外の人に、
「シャク」と言っても、
「ああシャコのこと。
シャコを九州では『シャク』っていうんだ。」
と言われてしまいます。
Wikipediaの「シャコ」の解説も間違っているので、
勘違いも仕方ないのかもしれませんが、
シャクとシャコは、別の種類の生き物。
分類も全く違います。
でも、
東京や関西の人に、
この美味しさを知られてしまうと、
手に入りにくくなるので、
勘違いしたままでいてもらいましょう

そういえば。。。
意外に熊本の人の中には、
「シャク」を「シャコ」のことだと思っている人もいるのかな~?
2013年07月03日
すうがくのえほん

「はじめて であう すうがくの絵本」
安野光雅さんの絵本です。
「さんすう」ではなく「すうがく」の絵本。
現代数学で扱う様々な問題の基礎を
安野光雅さんの絵で
イメージできる本です。
でも、
数字や計算はほとんどでききません。
子どもも大人も楽しく
「すうがく」の考え方に触れられる本です。
文章はすべてひらがな。
ひらがなを読める子は自分で、
ひらがなを読めない子は親子で
楽しめます。
ちなみに、
写真は以前の版の表紙です。
今、販売されている本の表紙は違うようです。
2013年06月10日
つるかめ算
息子のために、
夫がこんなものを作りました。

オリジナルの「つるかめ算」の問題です。
「つるかめ算」というと、
中学入試の算数にのみ使う知識、
という印象があります。
が、
夫に言わせると、
「問題を解く目の付け所のセンスを問う問題」だそうです。
たとえば、こんな問題。
「鶴と亀が合わせて50います。
足の数は、合わせて172です。
鶴は何羽、亀は何匹いますか?」
この問題を二次方程式で解くと、
鶴の数を X 、亀の数を Y として、
次の式を解くことになります。
・ X + Y = 50・・・①
・ 2X + 4Y = 172・・・②
①を変形して、
Y= 50-X
これを②に代入する。
2X + 4(50-X)=172
代入した式を解くと、
-2X =-28・・・③
この③の式は、
「鶴が1羽減ると、足が2本減る」ことを表す。
つまり、
問題文から読み取れる情報から
直接、③式を導くのが「つるかめ算」。
問題の情報のうち分からない数を
代数にして解くのが二次方程式。
夫、曰く、
「『つるかめ算』を分かっている方が、
代数を使った式の価値と意味が分かるだろうなあ。」
さて、オリジナルの問題。
息子が、お休みの日の朝食後、
「あ~、退屈だ~。」と嘆いている時に、
夫が息子へプレゼントしました

2013年04月23日
数の世界

最近、新聞で、
よく目にする本の広告です。
本の名前は、
「親子で楽しむ わくわく数の世界の大冒険」
とてもおもしろそうな本なので、
わがやでも購入を考えています。
ところで、
写真のかけ算の方法は、
「不思議~!」という感じもしますが、
実は、大人は、みんな、
学校で教わったことです。
中学校の数学ででてくる式、
(a-b)(a-c)
=aa-(ab+ac)+bc
この式を使った計算です。
ステップ1
この式の左辺を作ります。
94×97=(100-6)(100-3)
ステップ2
aa-(ab+ac)+bcの前半、
aa-(ab+ac)の部分を計算します。
aa-(ab+ac)=a(a-(b+c))なので、
(100-6)(100-3)では、
100×(100-(6+3))
となります。
この式の前半の「100×」が
広告の中では「百の位以上の数」と、
下線部は、「100-(6+3)=91」と
書かれています。
ステップ3
aa-(ab+ac)+bcの後半
bcの部分を計算します。
(100-6)(100-3)では、
6×3=18
となります。
中学校の数学の授業では、
式を覚えさせられるだけで、
こんな応用は教わりませんでした。。。
知っている知識の活かし方、
見方を変えたときのおもしろさを
大人も感じることができそうなので、
今度、書店に行った際に、
ちょっと中身を
のぞいてみようと思います。
ところで、
同じ単元で教わったもう1つの式
(a+b)の2乗=aa+2ab+bb
この式もいろいろ使えます。
以前、このブログでも紹介しています。
ぜひ、ご一読ください。
以前の記事は こちら です。
2013年04月07日
イカの刺身から学ぶ
昨晩のわがやの夕食に登場した
コウイカの刺身。
コウイカを調理する時に、
出てきたのがこれです。

コウイカの殻。
人間でいえば背骨にあたるところ、
かな?
先日、御船の恐竜博物館で、
息子は、
イカの御先祖様はアンモナイトということを学んでいたので、
すぐに、息子に見せました。
「このイカの殻はね、
アンモナイトの殻が、
小さくなったものって考えられてるんだよ。」
息子は興味津々。
そこで、次に、殻の造りを観察しました。
殻の断面を見ると。。。

息子は、
幾つもの層が重なっていることに気づきました。
人間の骨とは造りが違います。
アンモナイトの殻の中の造りを思い出し、
アンモナイトの殻を分けている壁と壁の間が狭くなったら、
どうなるかを考えると。。。
コウイカの殻の層のようになります
バネのこんなおもちゃがあると、
もっとこのことを実感できたかな~

息子は、
「学童(保育)のお友達は、
イカとアンモナイトが仲間って分かってくれんから、
学童にこれを持っていきたい。」
と言ってくれたので、
今回は、これでよかったのかな~
コウイカの刺身。
コウイカを調理する時に、
出てきたのがこれです。

コウイカの殻。
人間でいえば背骨にあたるところ、
かな?
先日、御船の恐竜博物館で、
息子は、
イカの御先祖様はアンモナイトということを学んでいたので、
すぐに、息子に見せました。
「このイカの殻はね、
アンモナイトの殻が、
小さくなったものって考えられてるんだよ。」
息子は興味津々。
そこで、次に、殻の造りを観察しました。
殻の断面を見ると。。。

息子は、
幾つもの層が重なっていることに気づきました。
人間の骨とは造りが違います。
アンモナイトの殻の中の造りを思い出し、
アンモナイトの殻を分けている壁と壁の間が狭くなったら、
どうなるかを考えると。。。

コウイカの殻の層のようになります

バネのこんなおもちゃがあると、
もっとこのことを実感できたかな~

息子は、
「学童(保育)のお友達は、
イカとアンモナイトが仲間って分かってくれんから、
学童にこれを持っていきたい。」
と言ってくれたので、
今回は、これでよかったのかな~

2013年03月19日
世界動物大図鑑
先週16日
日本経済新聞土曜版1面にて
おすすめの事典ベスト10が掲載されていました。
掲載されていた事典のうち、
我が家には、
9位と14位のものがあります。
そのうちの、
1冊、おすすめ14位が、
「世界動物大図鑑」です。

「動物」というと、
動物園にいる生き物を思い浮かべますが、
この事典には、
哺乳類、鳥類や爬虫類だけでなく、
魚類、無脊椎動物まで、
鮮やかな写真と
分かりやすい説明が
掲載されています。

概論や生息環境ごとの解説も
すばらしい
掲載されている動物は、
2,000種類以上
NHK「ダーウィンが来た」に登場する動物も
ほぼ網羅されているので、
番組を見た後に理解を深めるのにも役立ってます。
監修は、日高敏隆先生。
動物行動学の権威の方です。
秋篠宮殿下の推薦のお言葉も
眺めるだけで、
地球には、様々な動物が生きているんだな~、
と実感できる本です。
おすすめできない点があるとすると、
お値段が高めなことと写真かな~。
写真は、とてもきれいで、
それぞれの動物の特徴をよく捉えていますが、
リアル過ぎるのが・・・
虫嫌いな私は、虫のページにも触れません
日本経済新聞土曜版1面にて
おすすめの事典ベスト10が掲載されていました。
掲載されていた事典のうち、
我が家には、
9位と14位のものがあります。
そのうちの、
1冊、おすすめ14位が、
「世界動物大図鑑」です。

「動物」というと、
動物園にいる生き物を思い浮かべますが、
この事典には、
哺乳類、鳥類や爬虫類だけでなく、
魚類、無脊椎動物まで、
鮮やかな写真と
分かりやすい説明が
掲載されています。

概論や生息環境ごとの解説も
すばらしい

掲載されている動物は、
2,000種類以上

NHK「ダーウィンが来た」に登場する動物も
ほぼ網羅されているので、
番組を見た後に理解を深めるのにも役立ってます。
監修は、日高敏隆先生。
動物行動学の権威の方です。
秋篠宮殿下の推薦のお言葉も

眺めるだけで、
地球には、様々な動物が生きているんだな~、
と実感できる本です。
おすすめできない点があるとすると、
お値段が高めなことと写真かな~。
写真は、とてもきれいで、
それぞれの動物の特徴をよく捉えていますが、
リアル過ぎるのが・・・

虫嫌いな私は、虫のページにも触れません

2012年12月30日
絵本「絵で見るある港の歴史」
今回は、絵本の紹介です。
紹介するのは、「絵で見るある港の歴史」

2000年度ロングマン最優秀歴史書賞、
第48回産経児童出版文化賞大賞を受賞している
「絵で見るある町の歴史」とシリーズです。
ヨーロッパのどこかの入り江が
石器時代の夏の漁撈、物々交換の場から
現代の大都市に至る10,000年の歴史を
定点観測で描く絵本です。
その当時の船や建物、
人の服装、生活の様子が活き活きと
詳細に描かれています。
ローマ帝国の支配を受ける(150年ごろ)

新しい出発(950年ごろ)

定期市のたのしみ(1450年ごろ)

工業の発達(1890年ごろ)

大きくなった港(現在)

細かい点まで、史実に忠実に描きこまれているので、
時代時代の雰囲気を感じることができるし、
読むたびに新しい発見があります。
石器時代から現代まで
どの時代でも災難にあう男とその子孫が描かれています。
この男を探すのも、
「ウォーリーを探せ」みたいで楽しい
大人は歴史の本として、
子どもは絵本として、
どちらでも十分に堪能できる絵本。
親子で一緒に楽しめる絵本。。。
というより、
はじめは親子で楽しんでいても、
読み進むうちに、
パパがのめり込む絵本かもしれません
お正月に
親子で
こんな絵本をじっくり楽しむのもいいかな~
紹介するのは、「絵で見るある港の歴史」

2000年度ロングマン最優秀歴史書賞、
第48回産経児童出版文化賞大賞を受賞している
「絵で見るある町の歴史」とシリーズです。
ヨーロッパのどこかの入り江が
石器時代の夏の漁撈、物々交換の場から
現代の大都市に至る10,000年の歴史を
定点観測で描く絵本です。
その当時の船や建物、
人の服装、生活の様子が活き活きと
詳細に描かれています。
ローマ帝国の支配を受ける(150年ごろ)

新しい出発(950年ごろ)

定期市のたのしみ(1450年ごろ)

工業の発達(1890年ごろ)

大きくなった港(現在)

細かい点まで、史実に忠実に描きこまれているので、
時代時代の雰囲気を感じることができるし、
読むたびに新しい発見があります。
石器時代から現代まで
どの時代でも災難にあう男とその子孫が描かれています。
この男を探すのも、
「ウォーリーを探せ」みたいで楽しい

大人は歴史の本として、
子どもは絵本として、
どちらでも十分に堪能できる絵本。
親子で一緒に楽しめる絵本。。。
というより、
はじめは親子で楽しんでいても、
読み進むうちに、
パパがのめり込む絵本かもしれません

お正月に
親子で
こんな絵本をじっくり楽しむのもいいかな~

2012年12月11日
分数の割り算の教え方
さて、先日、紹介しました
夫による息子への分数の割り算の教え方。
その続きです。
夫は、息子に、前回紹介した方法で
1/2を1/4、1/3、1/5、1/6などで割る計算をさせていました。
でも、図で計算するのは、ちょっと面倒。
そこで、次に、息子に
分母を1にすると分子と比べやすいことに気付かせ
分母の分数(例 1/4)の分母と同じ数(例 4)を
分母と分子にかける計算を教えていました。
こんな感じです。

そして、
いよいよ、分数の割り算の式へ!!!
と、思いましたが、もう少し遠回り
ここまで、
息子には分子を1に統一した分数で計算させてきましたが、
ついに、「1」を卒業です。
1/2 を 5/8 で割ってみます。
ここで分母と分子を比べやすいように、
分母を「1」にするためには、
分母に逆数をかけていたことに気づかせ、
次の計算をさせます。

この計算を変形すると、
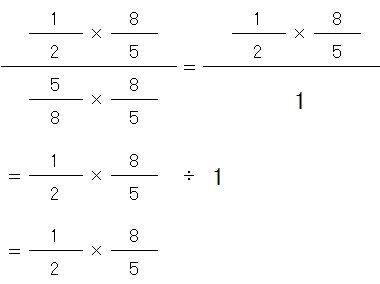
 分数の割り算の式、
分数の割り算の式、
割る数の逆数をかけるがでてきました。
なるほど~
夫の一言です。
「この式で重要なことは2つ。
「比べる」という割り算の本質を理解して、
比べる便宜のために分母を1にする操作をすること、
分数の割り算の式には「÷1」が隠れていること。
この2つをきちんと理解することの方が、
計算を早く正確にすることより大事」
だそうです。
自称「数学苦手」な夫が教える算数、
侮っていましたが、
なかなか奥が深いです
アーチを組める台形の積み木「 A R C H .」
熊本市現代美術館、 ザ・スタディールーム(東京、仙台、名古屋)、
通信販売 にて、お求めになれます。
詳しくはホームページにて。
↓の画像をクリックするとPC用ホームページが開きます


通信販売は、左の「オーナーへメッセージ」からも受け付けています
夫による息子への分数の割り算の教え方。
その続きです。
夫は、息子に、前回紹介した方法で
1/2を1/4、1/3、1/5、1/6などで割る計算をさせていました。
でも、図で計算するのは、ちょっと面倒。
そこで、次に、息子に
分母を1にすると分子と比べやすいことに気付かせ
分母の分数(例 1/4)の分母と同じ数(例 4)を
分母と分子にかける計算を教えていました。
こんな感じです。

そして、
いよいよ、分数の割り算の式へ!!!
と、思いましたが、もう少し遠回り

ここまで、
息子には分子を1に統一した分数で計算させてきましたが、
ついに、「1」を卒業です。
1/2 を 5/8 で割ってみます。
ここで分母と分子を比べやすいように、
分母を「1」にするためには、
分母に逆数をかけていたことに気づかせ、
次の計算をさせます。

この計算を変形すると、
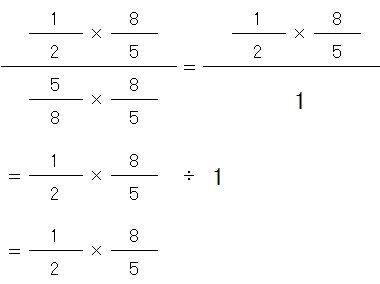
 分数の割り算の式、
分数の割り算の式、割る数の逆数をかけるがでてきました。
なるほど~

夫の一言です。
「この式で重要なことは2つ。
「比べる」という割り算の本質を理解して、
比べる便宜のために分母を1にする操作をすること、
分数の割り算の式には「÷1」が隠れていること。
この2つをきちんと理解することの方が、
計算を早く正確にすることより大事」
だそうです。
自称「数学苦手」な夫が教える算数、
侮っていましたが、
なかなか奥が深いです

アーチを組める台形の積み木「 A R C H .」
熊本市現代美術館、 ザ・スタディールーム(東京、仙台、名古屋)、
通信販売 にて、お求めになれます。
詳しくはホームページにて。
↓の画像をクリックするとPC用ホームページが開きます


通信販売は、左の「オーナーへメッセージ」からも受け付けています

2012年12月08日
分数の割り算
何がきっかけかわかりませんが、
息子が、ふと分数への興味を示しました。
これを見逃さなかったのが、
以前、予備校の講師をしていた教え魔の夫。
自分の担当科目でもなかったのに、
さっそく、6歳の息子へ分数を教え始めました。
「もう、そんなに慌てなくても 」と思いつつ、
」と思いつつ、
教えていることに耳を傾けると、
学校で教わったのとはちょっと違います。
まず、分数の意味を教えていました。
夫は、息子へ、
「分数は、分母から見た分子の大きさを表している」と教えていました。
(以下、夫から息子への説明の実況です)

分数4 / 2 を図にするとこんな感じ。

2からみると4は2が2個分の大きさだから、
4 / 2 = 2
でも、「2」って数字があるから、
普通は、わざわざ、2を 4 / 2とは書かないんだよ。
分数が役立つのは、1より小さい数字を表すとき。
たとえば、
1の半分は1/2、その半分を 1/4 だね。
図にすると、こんな感じ。

これが、分数ね。
さあ、今日は、これで終わり
と思いきや、
こともあろうか、夫は、6歳の息子に、
「分数の割り算をやってみる?」と尋ねました。
「えっ~~
分数の割り算って、小学校でも4年生か5年生でやるんじゃ???」
分数を理解できたことに自信をもった息子は、
無謀にも「やる!やる! 」と
」と
大張り切り。
夫の割り算の教え方にそっと聞き耳を(←どこかで聞いたこと?)
分数の割り算、1 / 2 ÷ 1 / 4 は、
中学校以上になると、
1 / 4(分母) 分の1 / 2(分子)と書くから、
これを使うね。
こう書くと、はじめの説明から考えると、
1 / 4 からみると、
1 / 2は、 1 / 4 が2つぶんの大きさ。

だから、答えは、「2」
その後、
夫は、1 / 2 をいろいろな分数で割り、
図を使い、息子に答えを考えさせ、
その結果を並べて、
分母になる分数の分母、
たとえば、1 / 2 ÷ 1 / 4 の場合、
4を分子、分母にかけると、
分母と分子の比較がしやすいことを
息子に気づかせていました。
夫によると、
分数の割り算の式を教えるのは、
もう少し先だそうです。
息子が、ふと分数への興味を示しました。
これを見逃さなかったのが、
以前、予備校の講師をしていた教え魔の夫。
自分の担当科目でもなかったのに、
さっそく、6歳の息子へ分数を教え始めました。
「もう、そんなに慌てなくても
 」と思いつつ、
」と思いつつ、教えていることに耳を傾けると、
学校で教わったのとはちょっと違います。
まず、分数の意味を教えていました。
夫は、息子へ、
「分数は、分母から見た分子の大きさを表している」と教えていました。
(以下、夫から息子への説明の実況です)

分数4 / 2 を図にするとこんな感じ。

2からみると4は2が2個分の大きさだから、
4 / 2 = 2
でも、「2」って数字があるから、
普通は、わざわざ、2を 4 / 2とは書かないんだよ。
分数が役立つのは、1より小さい数字を表すとき。
たとえば、
1の半分は1/2、その半分を 1/4 だね。
図にすると、こんな感じ。

これが、分数ね。
さあ、今日は、これで終わり

と思いきや、
こともあろうか、夫は、6歳の息子に、
「分数の割り算をやってみる?」と尋ねました。
「えっ~~

分数の割り算って、小学校でも4年生か5年生でやるんじゃ???」
分数を理解できたことに自信をもった息子は、
無謀にも「やる!やる!
 」と
」と大張り切り。
夫の割り算の教え方にそっと聞き耳を(←どこかで聞いたこと?)
分数の割り算、1 / 2 ÷ 1 / 4 は、
中学校以上になると、
1 / 4(分母) 分の1 / 2(分子)と書くから、
これを使うね。
こう書くと、はじめの説明から考えると、
1 / 4 からみると、
1 / 2は、 1 / 4 が2つぶんの大きさ。

だから、答えは、「2」
その後、
夫は、1 / 2 をいろいろな分数で割り、
図を使い、息子に答えを考えさせ、
その結果を並べて、
分母になる分数の分母、
たとえば、1 / 2 ÷ 1 / 4 の場合、
4を分子、分母にかけると、
分母と分子の比較がしやすいことを
息子に気づかせていました。
夫によると、
分数の割り算の式を教えるのは、
もう少し先だそうです。
















